数列の一般項の賢い求め方(問題付き)
数列が苦手な人はいませんか?
数列は公式を覚えただけでは解けないので、一見難しそうな単元です。
しかし、実は大事なポイントさえ押さえることができれば
とても面白い単元なのです。
ここでは「数列の一般項の求め方」を学習しましょう。
それはずばり
「数列がどのパターンに属するか」
数列は主に以下の4つのパターンに分類できます。
1.等差数列
2.等比数列
3.階差数列
4.その他(漸化式)
いずれのパターンに属するか見極めることができれば、一般項を求めたも同然です!
1.等差数列
【一定の差で増える(もしくは減る)】
一般項:an=a+(n̠̠-1)d
(例)1,3,5,7,9, ‥‥
2.等比数列
【一定の比で増える(もしくは減る)】
一般項:an=arn-1
(例)2,4,8,16,32, ‥‥
3.階差数列
【前の項と次の項の差に明らかな特徴がある】
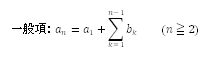
(例)2,3,5,8,12, ‥‥
4.その他(漸化式)
その他の一般項の求め方はこちらで説明しています。
それでは問題を解いていきましょう。
【問題】
次の数列の一般項を求めよ。
2,5,8,11, ‥‥
【考え方】
この数列は、3ずつ増えているので等差数列である。
【解答】
a(初項)=2, d(公差)=3 を代入して
an=2+(n-1)・3
=3n―1
【問題】
次の数列の一般項を求めよ。
1,3,9,27, ‥‥
【考え方】
前の項に3をかけると次の項になるので等比数列である。
【解答】
a(初項)=1, r(公比)=3を代入して
an=1・3n-1
=3n-1
【問題】
次の数列の一般項を求めよ。
1,2,6,15,31, ‥‥
【考え方】
後ろの項から前の項をひくと
1,4,9,16, ‥‥
=12,22,32,42, ‥‥
明らかな特徴があるので、階差数列である。
【解答】
bn=n2 であるので
a(初項)=1, bn=n2 を代入して
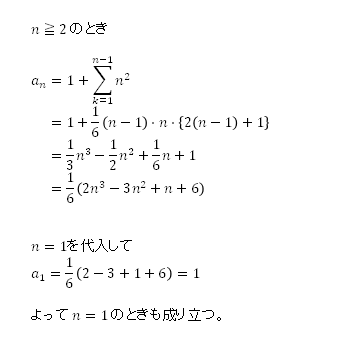
【問題】
次の数列の一般項を求めよ。
a1=1, an+1=2an-3
【考え方】
この数列は、等差数列でも等比数列でもない。
式もよくわからないので、
その他(漸化式)を用いて一般項を求める。(階差数列でも解けます!)
※解答は【漸化式の求め方】に記載しています。
By スタッフ01

