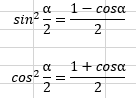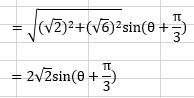三角関数の公式と語呂合わせまとめ(問題付き)
「数学Ⅱ|三角関数」の公式まとめです。
(下の方に練習問題があります。)
●加法定理
sin(α+β)=sinαcosβ+cosαsinβ
sin(α-β)=sinαcosβ-cosαsinβ
cos(α+β)=cosαcosβ-sinαsinβ
cos(α-β)=cosαcosβ+sinαsinβ
●2倍角
sin2α=2sinαcosα
cos2α=cos2α-sin2α
=2cos2α-1
=1-2sin2α
●半角
●和積の公式
和→積

積→和
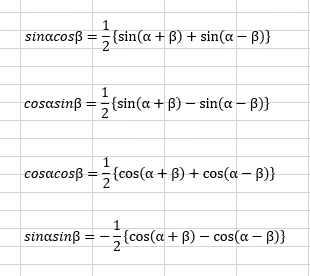
●合成
asinθ+bcosθ=(√a2+b2)sin(θ+α)
●加法定理
sinを「咲いた」、cosを「コスモス」に置き換えます。
「咲いたコスモスコスモス咲いた」
sin(α+β)=sinαcosβ+cosαsinβ
sin(α-β)=sinαcosβ-cosαsinβ
「コスモスコスモス咲かない咲かない」←「咲かない」がポイント!符号が逆になります!
cos(α+β)=cosαcosβ-sinαsinβ
cos(α-β)=cosαcosβ+sinαsinβ
●和積の公式
① 師は信仰
師(sin)は(和)信(sin)仰(cos)
つまり【sinの和はsin,cos】
先生は敬えという意味かな‥‥たぶん。
② 師引っ越し
師(sin)引っ(-)越(cos)し(sin)
つまり【sinの差はcos,sin】
先生が引っ越してしまいました。
③ 子は孝行
子(cos)は(和)孝(cos)行(cos)
つまり【cosの和はcos,cos】
子は孝行しなさいということかな。
④ 子引く負け獅子
子(cos)引く(-)負け(-)獅(sin)子(sin)
つまり【cosの差は-をつけてsin,sin】
子が綱引きをして獅子に負けたと。それとも獅子が負けたのか?どういう状況よこれ。
とまあ、そんな感じで
語呂合わせは覚えていたほうが便利です。
それでは公式を覚えたか、練習問題で確認してみましょう。
【問題】
0<α<( π/2)<β<π である。
sinα=2/3,sinβ=3√5/7のとき,sin(α+β) の値を求めよ。
【考え方】
sin(α+β)=sinαcosβ+cosαsinβ
【解答】
cos2α=1-sin2α=1-(2/3)2=5/9
0<α< π/2 であるから
cosα>0
よって
cosα=√5/3
また
cos2β=1-sin2=1-(3√5/7)2=4/49
π/2<β<π より
cosβ<0
よって
cosβ=-2/7
ゆえに
sin(α+β)=sinαcosβ+cosαsinβ
=(2/3)(-2/7)+(√5/3)(3√5/7)
=11/21
【問題】
0<α<π/2 である。
sinα=2/3 のとき,sin2α の値を求めよ。
【考え方】
sin2α=2sinαcosα
【解答】
cos2α=1-sin2α=1-(2/3)2=5/9
0<α<π/2 であるから
cosα>0
よって
cosα=√5/3
ゆえに
sin2α=2sinαcosα
=2・(2/3)・(√5/3)
=4√5/9
【問題】
0≦θ<2π であるとき、次の関数の最大値、最小値を求めよ。
f(θ)=√2sinθ+√6cosθ
【考え方】
関数を合成して考える。
【解答】
f(θ)=√2sinθ+√6cosθ
0≦θ<2π であるから
π/3≦θ+π/3<7π/3
sin(π/3)≦sin(θ+π/3)<sin(7π/3)
-1≦sin(θ+π/3)≦1
-2√2≦2√2sin(θ+π/3)≦2√2
よって
θ+π/3=π/2
θ=π/6 のとき最大
θ+π/3=3π/2
θ=7π/6 のとき最小をとる。
したがって
最大値 2√2(θ=π/6)
最小値 -2√2(θ=7π/6)
By スタッフ01