２次方程式の解の存在範囲（問題付き）

「２つの解がともに正であるとき・・・」「２つの解がともに１より小さいとき・・・」

こんな問題が、数学Ⅰの２次関数で出てきます。

どのようにして解いていますか？

ここではそんな「２次関数｜２次方程式の解の存在範囲」について説明します。

１．判別式
　　解の個数を確認します。（異なる２つの解：D＞０／２つの解：D≧０　など）

２．軸の位置
　　基準となる値と軸との位置関係を考えます。

３．ｆ(ｐ)の符号
　　基準となる値ｐに関して、ｆ(ｐ)の符号を考えます。（※「＝」が入るかどうかも丁寧に考えます。）

以上の３つを確認することで、取りこぼすことなく２次方程式の解の存在範囲を求めることができます。

それでは早速問題を解いてみましょう。

【問題】

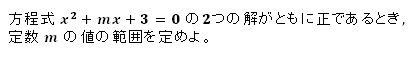
【考え方】
下に凸であるので、以下の３パターンが考えられる。
「２つの解がともに正」であるので、【Ⅲ】を求めたい。

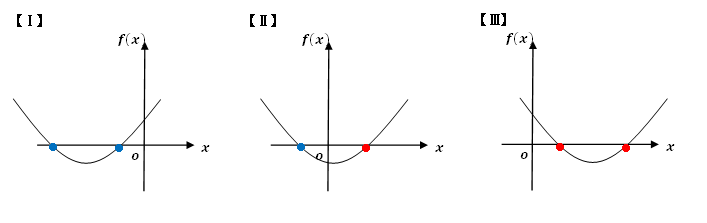
１．判別式
　　解が存在するので、判別式 D≧０
　　（２つの解は重解でも可）

２．軸の位置
　　
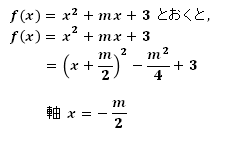
　　「２つの解がともに正」であるので、軸＞０

ここで【Ⅱ】【Ⅲ】に絞られる。

３．f(p)の符号
　　【Ⅱ】はｆ(０)＜０　　　【Ⅲ】はｆ(０)＞０
　　

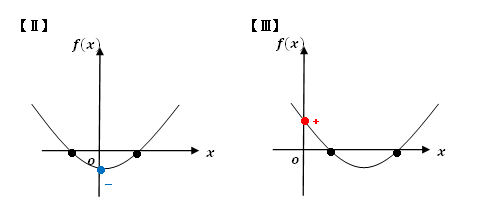
　　ちなみに、この問題の場合 y 切片は「３」であるので、
　　【Ⅱ】は最初から考えなくてよい。

【解答】

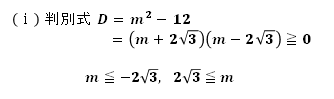
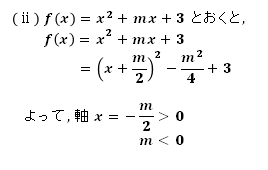
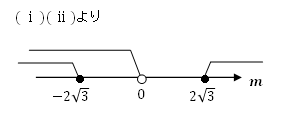
よって、m≦-２√３

By スタッフ01