【範囲編】文字を含む2次関数の最大値と最小値（問題付き）

ここでは「定義域に文字を含む２次関数の最大値・最小値」について説明します。

「ｙ＝ｘ²－４ｘ+３（ａ≦ｘ≦ａ＋１）」
↑こんなやつです。

最大値・最小値の求め方

１．グラフをかく。
　　「定義域に文字を含む２次関数の最大値・最小値」では式が決まっているため、
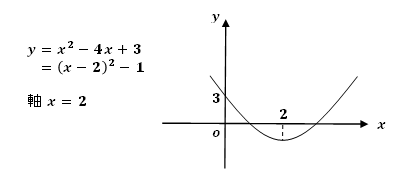
　　式を平方完成して「軸」を求め、グラフを描くことで視覚的に理解しやすくなります。

２．定義域の中央を確認する。
　　「軸」と「定義域／定義域の中央」との位置関係が重要になります。

３．定義域を移動させる。
　　定義域を「A.軸の左外」「B.軸上・定義域の中央が軸より左」「C.軸上・定義域の中央が軸上」
　　「D.軸上・定義域の中央が軸より右」「E.軸の右外」と移動させることで、
　　最大値・最小値の変化を確認します。

何言ってるんだ？？？？？？？

と思ってます？
大丈夫。
問題を解いていくうちに、少しずつ言っている意味が分かってくるはずです。

それでは実際に問題を解いてみましょう。

練習問題

【問題】

【考え方】
１．式を平方完成して軸を求め、グラフを記入する。

２．定義域の中央を確認

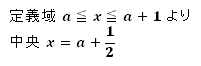
３．定義域を「A.軸の左外」「B.軸上・定義域の中央が軸より左」「C.軸上・定義域の中央が軸上」「D.軸上・定義域の中央が軸より右」「E.軸の右外」に移動する。

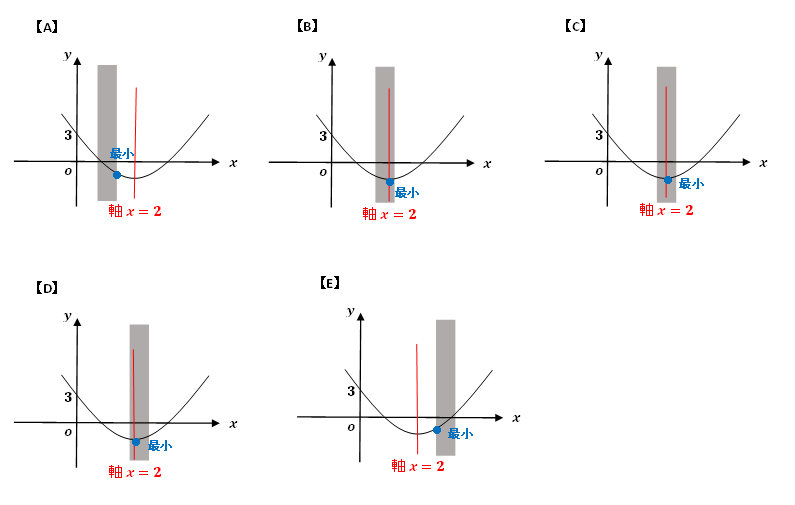
【A】ｘ＝ａ+１で最小
【B】ｘ＝２で最小
【C】ｘ＝２で最小
【D】ｘ＝２で最小
【E】ｘ＝ａで最小

※ちなみに
【A】ｘ＝ａで最大
【B】ｘ＝ａで最大
【C】ｘ＝ａ，ａ+１で最大
【D】ｘ＝ａ+１で最大
【E】ｘ＝ａ+１で最大

【解答】

意味が分かってきましたか？
分かってきたところで、持っている問題集などで練習してみてください。