【係数編】文字を含む2次関数の最大値と最小値(問題付き)
ここでは「係数に文字を含む2次関数の最大値・最小値」の求め方について解説します。
「y=-x2+6ax-a(0≦x≦3)」
↑こんなやつです。
1.グラフを書いて範囲を固定する。
「係数に文字を含む2次関数」の場合、定義域は固定されているため、
グラフに定義域を書くことで、視覚的に理解しやすくなります。
2.グラフが「上に凸」か「下に凸」か確認する。
どちらかによって、最大値・最小値の考え方が逆になります。
3.式を平方完成し、軸を求める。
「軸」と「定義域」の位置関係が重要になります。
4.軸と定義域の位置関係を考える。
グラフの軸を「定義域の左外」「定義域内・定義域中央より左」「定義域内・中央」
「定義域内・定義域中央より右」「定義域の右外」とずらしていき、
どこで最大値・最小値が切り替わるか考えます。
文字で見ただけではなかなか難しそうですね。
実際に問題を解いて、雰囲気を掴みましょう。
【問題】
![]()
【考え方】
1.グラフに定義域(0≦x≦3)を記入する。
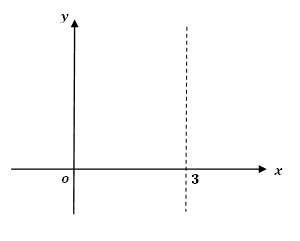
2.上に凸であることを確認
![]()
3.平方完成し、軸を求める。
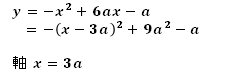
4.グラフの軸を「A.定義域の左外」「B.定義域内・定義域中央より左」「C.定義域内・中央」「D.定義域内・定義域中央より右」「E.定義域の右外」で考える。

【A】x=0 で最大
【B】x=3aで最大
【C】x=3a で最大
【D】x=3a で最大
【E】x=3で最大
※ちなみに
【A】x=3で最小
【B】x=3で最小
【C】x=0,3で最小
【D】x=0で最小
【E】x=0で最小
【解答】

【問題】
![]()
【考え方】
1.グラフに定義域(0≦x≦2)を記入する。
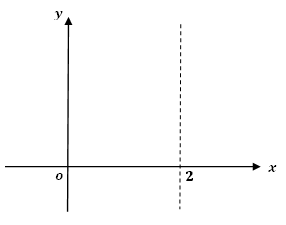
2.下に凸であることを確認
3.平方完成し、軸を求める。
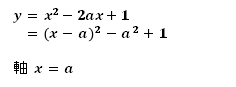
4.グラフの軸を「A.定義域の左外」「B.定義域内・定義域中央より左」「C.定義域内・中央」「D.定義域内・定義域中央より右」「E.定義域の右外」で考える。
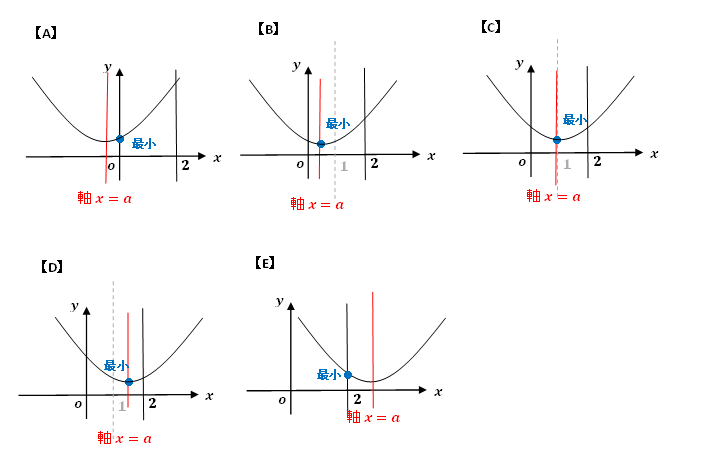
【A】x=0で最小
【B】x=aで最小
【C】x=aで最小
【D】x=aで最小
【E】x=2で最小
※ちなみに
【A】x=2 で最大
【B】x=2で最大
【C】x=0,2 で最大
【D】x=0 で最大
【E】x=0で最大
【解答】
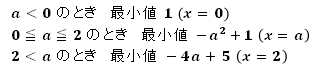
分かりましたか?
この単元は、根本をしっかりと理解することが重要です。
類題を探して解いてみてください。
もし分からなければ、周りの先生、友達に質問してみましょう。
もちろんMOTOゼミナールに質問してくれてもOKです!
By スタッフ01

