動く点と面積（問題付き）

中学２年生「１次関数」で学習する
「辺上を点が動くときの面積」について解説します。

こんなやつです。

①動く点Pの速さを確認し、ｘ秒後に何cm進んでいるか考える。
②辺上を動くのに何秒かかるか、辺ごとに考える。
③求める面積の形の変化を、辺ごとに考える。（面積が増加する・一定・減少するなど）
④求める面積の底辺、高さがどこになるか、辺ごとに考える。

ポイントは、時間・形の変化・辺の長さなどを「辺ごと」に考えることです。

それでは問題を解いてみましょう。

【問題】
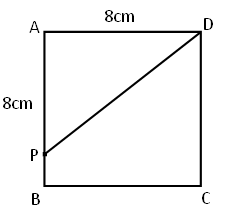
点Pは, １辺８cmの正方形ABCDの辺上を, AからB,Cを通ってDまで毎秒１cmの速さで動く。
点PがAを出発してからｘ秒後の△APDの面積をｙ㎠とするとき,ｘとｙの関係を式に表しなさい。

【考え方】
点Pは１辺８cmの辺上を毎秒１cmの速さで動くので、ｘ秒後にｘcm進んでおり、１辺を動くのに８秒かかる。
①点Pが辺AB上を動く：△APDは増加し、「底辺AD（８cm）、高さAP（ｘcm）」の三角形
②点Pが辺BC上を動く：△APDは一定、「底辺AD（８cm）、高さ点PからADにおろした垂線（８cm）」の三角形
③点Pが辺CD上を動く：△APDは減少し、「底辺AD（８cm）、高さDP（８cm×３－ｘcm）」の三角形

【解答】

【問題】
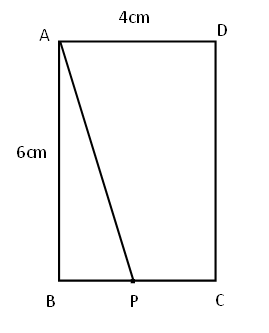
点Pは, AB＝６cm, BC＝４cmの長方形ABCDの辺上を, BからC,Dを通ってAまで毎秒２cmの速さで動く。
点PがBを出発してからｘ秒後の△ABPの面積をｙ㎠とするとき,ｘとｙの関係を式に表しなさい。

【考え方】
点Pは毎秒２cmで動くので、ｘ秒後に２ｘcm進んだことになる。
また、点Pは辺BC上を２秒、辺CD上を３秒、辺DA上を２秒でそれぞれ動く。
①点Pが辺BC上を動く：△ABPは増加し、「底辺BP（２ｘcm）、高さAB（６cm）」の三角形
②点Pが辺CD上を動く：△ABPは一定、「底辺AB（６cm）、高さ点PからABにおろした垂線（４cm）」の三角形
③点Pが辺DA上を動く：△ABPは減少し、「底辺AB（６cm）、高さAD（４cm＋６cm＋４cm－２ｘcm）」の三角形

【解答】

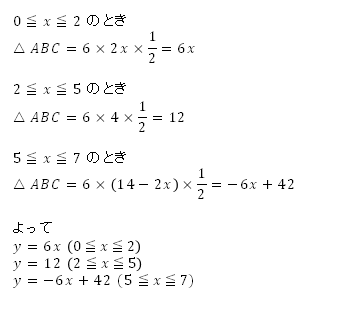
By スタッフ01